Quantum Maths for Single Qubit

Inner Product and Measurement - Born’s Rule

For given matrices $u$ and $v$, The inner product is given as (\(u^T\) is transpose of matrix \(u\)):

\[⟨u,v⟩ = u^Tv\]

Given state vectors of qubits as \(u\) and \(v\), the probability of measuring \(u\) in $v$ is the square of inner product of \(u\) and \(v\) is given as:

\[prob(\text{measuring state u in state v}) = (u.v)^2\]

It can also be said that:

\[prob(\text{measuring state u in state v}) = prob(\text{measuring state v in state u})\]

Inner product can be done easily with bra-ket notations and can be show with following table:

\[\begin{aligned} &\begin{array}{cccc} \hline \hline \text { Notation } & \text { Value }\\ \hline \bra{0}\ket{0} & 1 \\ \bra{1}\ket{1} & 1 \\ \bra{1}\ket{0} & 0 \\ \bra{0}\ket{1} & 0 \\ \bra{+}\ket{0} & \frac{1}{\sqrt{2}} \\ \bra{+}\ket{1} & \frac{1}{\sqrt{2}}\\ \bra{-}\ket{0} & \frac{-1}{\sqrt{2}}\\ \bra{-}\ket{1} & \frac{-1}{\sqrt{2}}\\ \hline \end{array} \end{aligned}\]

Hence, Born’s rule for bra-ket notations is give as follows:

\[prob(\text{measuring state a in b}) = |\bra{a}\ket{b}|^2\]

Gates as Matrices

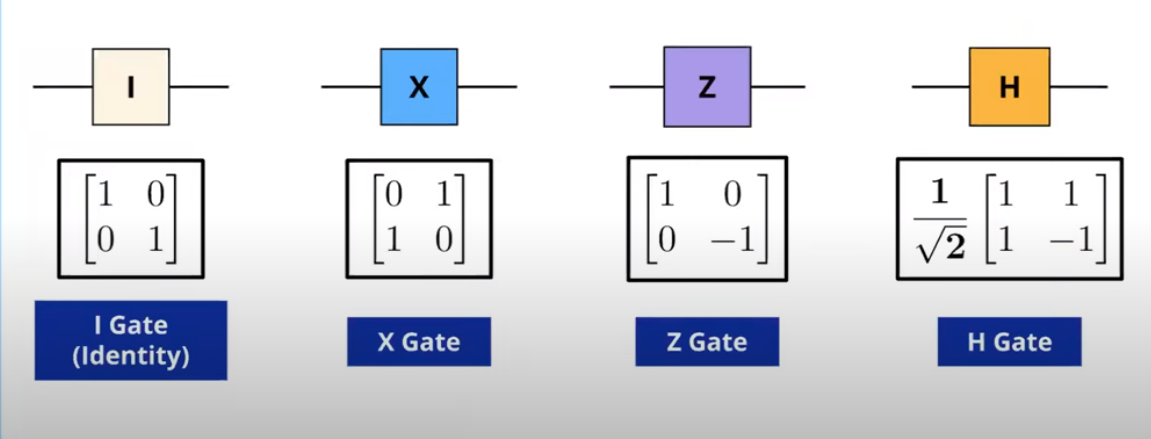
The transformation go quantum states using gates is given by: \(\text{Gate * State} = \text{New State}\)