Multi Qubit Maths

Tensor Product

Tensor state is used to combine quantum states to represent multiple systems at once. This is given below for matrix A and B: \(\mathbf{A} \otimes \mathbf{B} = \begin{bmatrix} A_{1,1} \mathbf{B} & \cdots & A_{1,n} \mathbf{B} \ \vdots & \ddots & \vdots \ A_{m,1} \mathbf{B} & \cdots & A_{m,n} \mathbf{B} \end{bmatrix}\)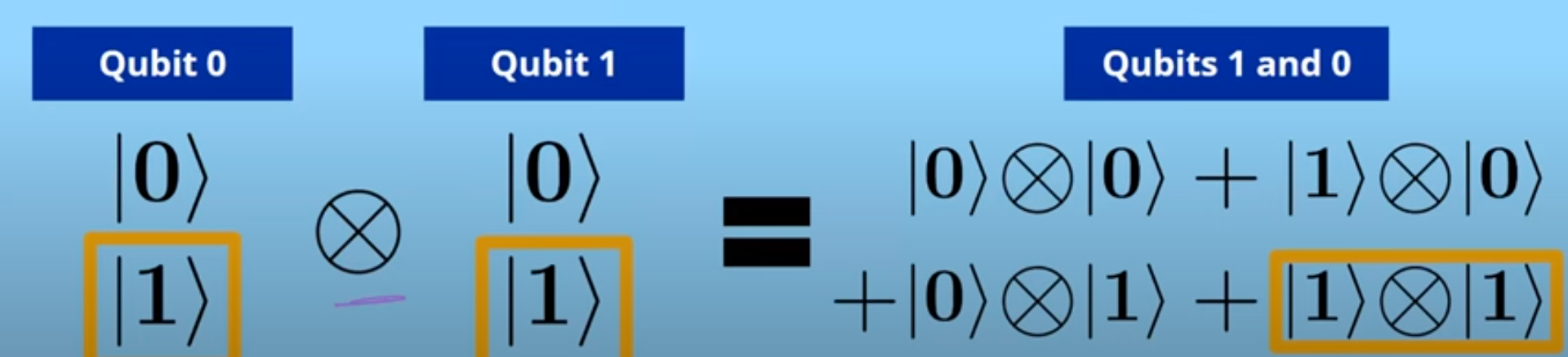

Missing States in Quantum Mechanics

States which can be represented as tensor products are called as Separable States on the other hand those states which cannot be represented as separable are Non-Separable States which none other than the Entangled State.

Ex: \(\frac{1}{\sqrt{2}} (\ket{00} + \ket{11})\) can be represented as tensor product

Few famous states are Bell States and GHZ States. Here are the Bell states:

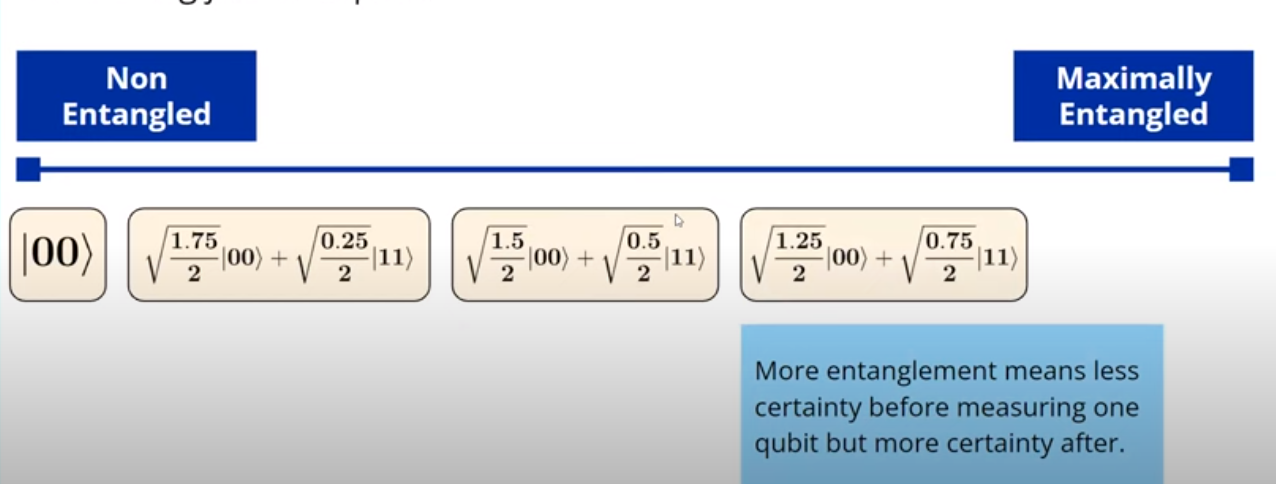
\[\begin{align*} |\psi_{BB84}\rangle &= \left\{ \begin{array}{c|c} \frac{1}{\sqrt{2}} & |00\rangle \\ \hline \frac{1}{\sqrt{2}} & |11\rangle \\ \hline 0 & \text{otherwise} \end{array} \right. \\ \\ |\psi_{B2}\rangle &= \left\{ \begin{array}{c|c} \frac{1}{\sqrt{2}} & |01\rangle \\ \hline \frac{1}{\sqrt{2}} & |10\rangle \\ \hline 0 & \text{otherwise} \end{array} \right. \\ \\ |\psi_{B3}\rangle &= \left\{ \begin{array}{c|c} \frac{1}{\sqrt{2}} & |00\rangle \\ \hline -\frac{1}{\sqrt{2}} & |11\rangle \\ \hline 0 & \text{otherwise} \end{array} \right. \\ \\ |\psi_{B4}\rangle &= \left\{ \begin{array}{c|c} \frac{1}{\sqrt{2}} & |01\rangle \\ \hline -\frac{1}{\sqrt{2}} & |10\rangle \\ \hline 0 & \text{otherwise} \end{array} \right. \end{align*}\]

Entanglement as a Spectrum